최대 (연속) 부분 배열 문제

🔑Table of Contents

1. 문제정의 
2. 알고리즘
3. 알고리즘1 - 기본아이디어
4. 알고리즘1 - 시간 복잡도 분석
5. 알고리즘2 - 기본 아이디어
6. 알고리즘2 - 시간 복잡도 분석
7. 순환 알고리즘 완성하기
8. 알고리즘3 - 분할정복법
9. 시간 T(n) 구하기
10. 알고리즘4 - 기본 아이디어
11. 알고리즘4 - 동적계획법 → O(n)

---

 

📌문제정의 

길이 n인 배열 A[0], A[1], ... , A[n-1]이 입력으로 주어질때, i번째부터 j번째 까지 원소들로 이루어진 배열 A[j], ..., A[j]를 부분 배열이라고 하고 A[i,j]로 나타냄 → A[0]도 존재함

 

• 문제는 최대 부분 배열, 즉 부분 배열에 속한 원소들의 합이 최대가 되는 부분 배열을 찾는 것이다 

이때, 길이가 0인 부분 배열도 허용하며, 이 부분배열의 원소들의 합은 0이라고 정의함

 

• 예를들어 +31, -41, +59, +26, -53, +58, +97, -93, -23, +84 와 같은 배열이 있을때 최대 부분 배열은 A[2,6] 이때 원소들의 합(=크기)은 187이다 

📌알고리즘

최대 부분 배열의 원소합을 구하는 알고리즘 

   • 알고리즘 1 = 단순한 O(n³) 알고리즘

   • 알고리즘 2 = 중복 계산을 제거한 O(n²) 알고리즘

   • 알고리즘 3 = O(n logn) 분할정복법 알고리즘

   • 알고리즘 4 = O(n) 동적계획법 알고리즘 

↓ 이론상 시간 줄어들음

위의 알고리즘을 조금만 수정하면 최대 부분 배열도 쉽게 구할수 있다 

 

📌알고리즘1 - 기본 아이디어

모든 가능한 부분 배열 각각에 대해서 원소합을 계산해 그들의 최대값을 구한다 

부분배열은 A[i, j]로 나타내며, 이때 0 ≤ i ≤ j ≤ n-1이 된다 

  • ThisSum은 현재 고려하고 있는 부분배열의 원소합

  • MaxSum은 현재까지 고려한 부분 배열의 최대 원소합을 보관한다 

두수의 최대값을 돌려주는 함수나 마크로 max( )를 정의한다 

 

모든 경우의 수 비교

A[0] ㅁ ㅁ ㅁ ㅁ ㅁ A[n]

 

1) ThisSum + A[k] 대입                                      n번

0

0 + I----I

0 + I--------I → k가 j번까지 , j는 n까지

.

...

2) 대입한 ThisSum을 MaxSum과 비교후 대입   n번

3) 1,2번 과정을 A[0] ~ A[n]까지                          n번            → O(n³)

 

→ 장점 : 생각하기 쉬움, 단점 : 중복이 많음

 

k번째 원소의 메모리 주소

base(A의 주소) + 4 × k (4는 int형의 바이트 수)

 

시간 복잡도 분석

코드 전체 시간은 n(12n² + 16n + 5) + n(3n+1) + 3n + 3   결국, O(n³)로 귀결됨 

 

📌 알고리즘1 - 시간 복잡도 분석

i for문 n번반복 j for문 n-i회 반복  (0 ≤ i ≤ n-1) 이 성립하기에 n회 이하 반복 가장 안쪽 for문은 j-i+1회 반복 실행되나 (0 ≤ i ≤ j ≤ n-1)이므로 n회 반복 

• 알고리즘 시간 복잡도 분석
  • 가장 안쪽 for문은 덧셈, 치환 반복해 O(n)
  • 가운데 for문은 O(n) 시간의 for문과 O(1)시간을 쓰는 비교 및 치환을 최대 n회 반복해 O(n²)
  • 바깥 for문은 O(n²) 시간의 for문을 n회 반복해 O(n³)가 됨 
• 분석이 느슨한가? 
  • 상계를 이용해 시간복잡도 O(n³)를 구함
  • k for문의 실행횟수를 구해보자
    • 실행횟수는 다음과 같다 

 

📌알고리즘2 - 기본 아이디어

계산이 중복되는 부분을 찾아 제거해 보다 효율적인 알고리즘을 만드는것이 중요하다 

알고리즘1을 관찰하면 중복해 계산하는 부분이 있다는 것을 알수있다 A[i, j]의 원소합을 A[i, j-1]의 원소합으로 구할수있다

즉, 이렇게 하면 기존 O(n³)에서 **중복 계산 제거하면 O(n²)**까지도 줄일 수 있음

 

int MaxSubarray(int A[], int n)
{
    int MaxSum, ThisSum;
    int i, j;
    MaxSum = 0;

    for (i = 0; i < n; i++) {
        ThisSum = 0;
        for (j = i; j < n; j++) {
            ThisSum = ThisSum + A[j];      // 누적합
            MaxSum = max(MaxSum, ThisSum); // 최대값 갱신
        }
    }return MaxSum;
}

1️⃣ ThisSum 대입 후 MaxSum 비교 n+1

2️⃣  A[0]부터 A[n]까지 1️⃣ n번                   →O(n²)

 

📌알고리즘2 - 시간 복잡도 분석

부분배열 A[i, j]의 원소합을 A[i,j-1]의 원소합으로 부터 O(1)시간에 구했다 이로인해 삼중for → 이중 for로 줄일수 있었음

이 개선된 알고리즘의 시간복잡도는 얼마나 얼마나 될까 

알고리즘2의 시간복잡도가 o(n²)임을 보여라 

 

🤔 

알고리즘2는 모든 부분배열을 고려한다

부분배열의 총 개수는 Θ(n²)개이다. 왜냐하면 i ≠ j인 부분배열이 (n 2)개 있고 i = j인 부분배열이 n개있기 때문이다 

 

Θ(n²)보다 더 빠른 알고리즘을 설계하려면 어떻게해야할까??

순환을 이용해 설계할까?

• 배열 A[0], ... , A[n-1]을 두 부분으로 나눠보자 
  • A[0], ... , A[k]   |   A[k+1], ... , A[n-1]
• 배열 A[0, n - 1]에 대한 최대 부분 배열
  • 배열의 앞부분에 속하거나
  • 배열의 뒷부분에 속하거나 
  • A[k]와 A[k+1]을 포함해 앞뒤에 걸쳐있다 
• 세 경우를 각각 최대 부분 배열을 구해 셋중에서 최대를 취하면 원래 배열에 대한 최대 부분 배열이 된다 
• 앞부분에 속한 최대 부분 배열은 배열 A[0,k]에 대한 최대 부분 배열이므로 순환호출을 이용해 구한다
• 배열 뒷부분도 마찬가지로 순환호출을 이용한다 
• 앞뒤에 걸쳐있는 최대 부분 배열은 어떻게 효율적으로 구할까
  • 앞뒤에 걸쳐있는 부분배열은 (k + 1)(n - k - 1)개가 되는데 이것을 모두 고려해야할까?
  • 배열의 앞부분에서 A[k]를 포함하는 최대 부분배열을 구하고 배열의 뒷부분에서 A[k+1]을 포함하는 최대부분 배열을 구한다음 , 두 부분배열을 하나로 묶으면 앞뒤에 걸쳐있는 최대 부분 배열이 된다 
    • A[k]를 포함하는 부분 배열은 k + 1개가있음 (A[0,k], ... , A[i,k],A[i+1, k], ... , A[k,k])
    • A[i,k]의 원소합은 A[i+1, k]의 원소합이 주어져 있으면 (i+1,k)A[j] + A[i] 

📌 순환 알고리즘 완성하기

그러면 k를 얼마로 정할것인가?

• 앞부분과 뒷부분에 속한 원소의 수가 거의 같도록 나누자
• 사실 0 < α < 1을 만족하는 α 에 대해서 αn과 (1- α)n으로 나누어도 시간복잡도가 달라지지는 않지만 일반적으로 반씩 나누는게 좋음

MaxSubarray(A, i, j)를 호출함으로써, A[i, j]의 최대부분배열의 원소합을 구하도록한다 

• 배열에 속한 원소가 1개이면 그것이 양수인지 음수인지를 판단해 양수이면 그 값을 음수이면 0을 반환한다 
• 원소가 2개 이상이면 순환 호출한다 

           Max C를 찾고   Max L, Max R은 재귀로 찾기   → Max L, Max R, Max C 중 최대값 찾기 

           →재귀불가       → (임의의 인덱스[재귀가능])

 

🔖Max C 구하기 

n/2개 중 가장 큰거 구하는 방법이 젤 좋음 → n/2 + n/2 = n → O(n)

<<n/2 * n/2 = n²/4 = O(n²) >> 이렇게 한번에 구하는 방법은 좋지 않다

 

 

 

📌알고리즘3 - 분할정복법

int MaxSubarray ( int A[ ], int Left, int Right){
  int MaxSum, MaxLeft, MaxRight, MaxCenter;
  int MaxCenterL, MaxCenterR, ThisSum;
  int Center, i;
  
  if (Left == Right) {
    if (A[Left] > 0) return A[Left];
    else return 0;
  }
  
  Center = (Left + Right) / 2;
  MaxLeft = MaxSubarray(A, Left, Center);
  MaxRight = MaxSubarray(A, Center + 1, Right);
  
  MaxCenterL = 0;
  ThisSum = 0;
  for (i = Center; i >= Left; i--) {
    ThisSum += A[i];
    MaxCenterL = max(MaxCenterL, ThisSum);
  }
  
  MaxCenterR = 0;
  ThisSum = 0;
  for (i = Center + 1; i <= Right; i++) {
    ThisSum += A[i];
    MaxCenterR = max(MaxCenterR, ThisSum);
  }
  MaxCenter = MaxCenterL + MaxCenterR;
  MaxSum = max(max(MaxLeft, MaxRight), MaxCenter);
  return MaxSum;
}

T(n) = 길이가 n인 배열에서 최대부분 배열을 구하는데 걸리는 시간

n = 1일 때는 단지 if문을 수행하므로 상수 시간이다 

n ≥ 2인 경우에는 배열을 반으로 나누어 길이가 n/2인 배열 각각에 대해 순환 호출을 한다 

두개의 for문을 수행하는데 각각 O(n)시간 걸리기 때문에 나머지 시간 = O(n)

 

즉, T(n) = { O(1)  <n=1인경우>  , 2 • T(n/2) + O(n)  <n ≥ 2인경우>

 

📌 시간 T(n) 구하기

n을 

 

이라고 가정하면(2의 거듭제곱 근처로 맞춰 분석을 단순화하기위함)

 

 

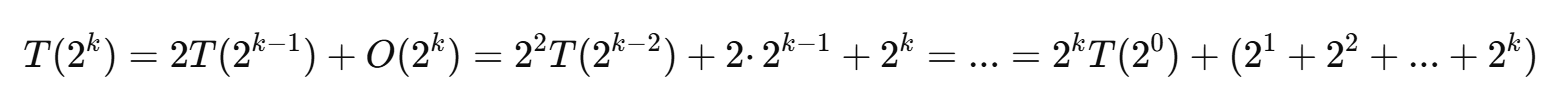
결과적으로 

 

k와 n 관계 정리

 

 즉, k = O(log n) 이된다 

 

최종결과

 

결론 : 시간복잡도는 

 

 

 

📌알고리즘4 - 기본 아이디어

부분배열의 오른쪽 끝이 A[k]인 최대 부분 배열의 원소합을 s[k]라고하자 

s[k] → k+2개 부분 배열 중 최대 원소합 (A[0], ...,A[k] : k+1개 + s[k]=0 <아무것도 선택안한 것>)

 

s[0], s[1] , ... , s[n-1]을 모두구할 수 있으면 최대 부분 배열의 원소합은 이들 중에서 최대값이 된다 

(s[0] : A[0] ,s[1] : A[0][1], ... , s[n-1] : A[0]...[n-1])

 

 

🤔s[k]을 어떻게 구할 수 있을까? 

s[k-1]을 알고 있으면 다음과 같이 구할 수 있다 

s[k] = max{S[k - 1] A[k] , 0}

 

증명 → (오른쪽 끝이 A[k]인 최대 부분 배열의 길이는 0이거나 1 이상이다)

• 길이가 0인경우 : s[k] = 0
• 길이가 1 이상인 경우 그 최대 부분 배열의 맨 끝에 있는 원소 A[k]를 제거하면 오른쪽 끝이 A[k-1]인 최대 부분 배열임
  • 그렇지 않으면, 합이 더 큰 부분 배열의 오른쪽에 A[k]를 붙이면 합이 보다 더 큰 부분배열을 얻을 수 있어서 모순

int MaxSubarray(int A[ ], int n){
  int MaxSum, ThisSum;
  int k;
  
  MaxSum = 0;
  ThisSum = 0;
  for (k=0; k<n; k++){
    ThisSum = max(ThisSum + A[k] , 0);
    MaxSum = max(MaxSum, ThisSum);
  }
  return MaxSum;
}

 

📌알고리즘4 - 동적계획법 → O(n)

 

핵심개념 

• ThisSum : 현재까지의 누적합
• MaxSum : 전체 중 최대합 
• 만약 ThisSum + A[k]가 음수가 되면 버리고(0) 다시 시작 

 

예시1

A = [0 ,3, -2, -7, 10 ]

k	A[k]	ThisSum 계산	TS	MS
0	0	max(0+0,0)	0	0
1	3	max(0+3,0)	3	3
2	-2	max(3+(-2),0)	1	3
3	-7	max(1+(-7),0)	0	3
4	10	max(0+10,0)	10	10

∴ s[n] = A[4]   , Max = 10

 

예시2

A = [0 ,3, -2, 7, 10 ]

k	A[k]	ThisSum 계산	TS	MS
0	0	max(0+0,0)	0	0
1	3	max(0+3,0)	3	3
2	-2	max(3+(-2),0)	1	3
3	7	max(1+7,0)	8	8
4	10	max(8+10,0)	18	18

∴ s[n] = A[4]   , Max = 18

 

예시3

A = [9 ,3, -2, -7, 10 ]

k	A[k]	ThisSum 계산	TS	MS
0	9	max(0+9,0)	9	9
1	3	max(9+3,0)	12	12
2	-2	max(12+(-2),0)	10	12
3	-7	max(10+(-7),0)	3	12
4	10	max(3+10,0)	13	13

∴ s[n] = A[4]   , Max = 10

 

예시4

A = [-2 ,3, -2, 7, 10 ]

k	A[k]	ThisSum 계산	TS	MS
0	-2	max(0+(-2),0)	0	0
1	3	max(0+3,0)	3	3
2	-2	max(3+(-2),0)	1	3
3	7	max(1+7,0)	8	8
4	10	max(8+10,0)	18	18

∴ s[n] = A[4]   , Max = 10