leehyeon-dv 님의 블로그
3.5 Floating Point 본문
🔑Table of Contents
- Floating Point - 부동소수점
- Floating Point Standard - IEEE이론
- IEEE Floating-Point Format - IEEE계산방법,예제
- Single-Precision Range - 단정도 범위
- Double-Precision Range -배정도 범위
- Floating-Point Precision - 부동소수점의 정밀도
- Floating-Point Example
- Denormal Number - 비정규 숫자
- Infinities and NaNs - 무한대와 숫자가 아닌것
- Floating - Point Addition - 부동소숫점 덧셈
- FP Adder Hardware - 부동소수점 가산기
- Floating-Point Multiplication - 부동소수점 곱셈
- FP Arithmetic Hardware - 부동소수점 산술 하드웨어
- FP Instructions in MIPS - 부동소수점 MIPS명령어
- 궁금한점
📌Floating Point (부동소수점)
- 정수가 아닌 수(실수)를 표현하기 위해
- scientific notation (정수부가 일의 자리인 표현을 정규화된(normalized)표현)
- -2.34 * 10^56 (normalized) = -2.34e56
- 0.002 * 10 ^ (-4) (not normalized) = 2.0e-7
- 987.02 * 10^9 (not normalized) = 9.8702e11
- 289.375 => 2.89375 * 10^-2
- binary로는
- ±1.xxxxxxx_2 * 2^(yyyy)
- C언어에서 float형과 double형이라는 타입이 있다
📌Floating Point Standard
- IEEE(전기전자기술자협회)에 의해 IEEE 754로 정의됨
- 표현하는 방식이 많아지게 되자 개발됨
- 현재 대부분 보편적으로 채택하고있음
- 2개의 표현법 (single-precision(단정도,32bit), double-precision(배정도, 64bit)
※그 외
- half-precision: 16bit
- quadruple-precision : 128 bit
- octuple-precision: 256 bit
📌 IEEE Floating-Point Format

부호 지수 소수
💡공식 외우기

- 부호비트
- 0: 양수 / 1: 음수
- 지수
- 숫자의 크기를 결정하는 부분으로 , 초과표현을 사용
- 지수 = 실제지수 + Bias(편향지수)
- Single-Precision(단정밀도): Bias = 127
- Double-Precision(배정밀도) : Bias = 1023
- 가수 (소수-> 부동소수점 수의 정밀도를 결정하는 중요한 부분이다)
- 정규화(Normalization)되고 범위 : 1.0 ≤ |significand | ≤ 2.0
- 이진수로 표현될때 항상 1로 시작하는 비트가 존재 (hidden bit)
- 숨겨진 비트를 포함하면, 가수는 1.xxx의 형태가 된다
- 예를 들어, 가수 값이 0.1101이면 실제값은 1.1101이 된다
📝예제1(32 bit)
x = -6.5
- s = 1(음수)
- Fraction
- 6.5 = 110.1 = 1.101 * 2^2 (지수 → 2)
- 소수 = 0.101(2진수) → 0.5 + 0.125 = 0.625
- 가수 = 1+ 0.625 = 1.625
x=(−1)^1×1.625×2^2
결과 : IEEE 754 32비트 표현
부호(1)/지수(127+2=129)/소수(0.101)
1 10000001 10100000000000000000000
📝예제2(64 bit)
x = -25.75
- s = 1
- Fraction(2진수 변환)
- 25 = 11001
- 0.75 = 0.11
- 25.75 = 11001.11
- 정규화 → 1.100111 * 2^4 (지수 → 4)
- 가수 = 1.100111 = 1 + 0.5 + 0.0625 + 0.0078125 = 1.609375
- x = (−1)^1×1.609375×2^4
결과 : IEEE 754 64비트 표현
부호(1)/지수(1023 + 4 =1027)/소수(0.100111)
1 10000000011 1001110000000000000000000000000000000000000000000000
📌Single-Precision Range
단정도 범위
- exponent(멱지수)는 0000001(2)이상 11111110(2)이하 ( 00000000, 11111111은 사용되지 않는다)
- 가장작은값 ( 00000001) → 실제 Exponent : 1 - 127 = -126
- Fraction : 0000...
- Manissa(가수) : 1.0
- ±1.0 * 2^(-126) = ±1.8 * 10^(-38) 과 같이 계산됨
- 가장 큰값(11111110) → 실제 Exponent : 254 - 127 = 127
- Fraction : 1111...
- Manissa(가수) : 1.1111...111
- ±2.0 * 2^(127) = ±3.4 * 10^(38) 과 같이 계산됨
📌 Double-Precision Range
배정도 범위
- exponent(멱지수)는 0000001(2)이상 11111110(2)이하 ( 00000000, 11111111은 사용되지 않는다)
- 가장작은값 ( 00000001) → 실제 Exponent : 1 - 1023 = -1022
- Fraction : 0000...
- Manissa(가수) : 1.0
- ±1.0 * 2⁻¹⁰²² = ±2.2 * 10⁻³⁰⁸ 과 같이 계산됨
- 가장 큰값(11111110) → 실제 Exponent : 2046 - 1023 = 1023
- Fraction : 1111...
- Manissa(가수) : 1.1111...111
- ±2.0 * 2¹⁰²³ = ±1.8 * 10³⁰⁸ 과 같이 계산됨(참고)
📌 Floating-Point Precision
부동소수점의 정밀도 → Fraction 비트로 결정(많을수록 더 정확한 숫자표현가능)
- Relative precision (상대적인 정도 . 정확도)
- 모든 fraction 비트는 significant
- single: fraction이 23비트. 2⁻²³의 정확도
- 10진법 반환 → 23 * log2 ≈ 23 * 0.301 = 6.9 → 6~7자리까지 표현가능
- double : fraction이 52비트 2⁻⁵²의 정확도
- 10진법 반환 → 52 * log2 ≈ 52 * 0.301 = 15.65 → 15~16자리까지 표현가능(참고)
📌Floating-Point 예제
📝-0.75
- 2진법 = -0.11
- 정규화된 표현 = -1.1 * 2⁻¹
- 부호(S) = 1
- 가수 = 1.1
- 지수 = -1
- 부동소수점 표현
- 부호(S) = 1
- 가수 = 1000...00
- 지수 → single Precision(32bit) = -1 + 127 = 126 → 01111110
- → Double Precision(64bit) = -1 + 1023 = 1022 = 01111111110
- 결론
- single Precision = 1 01111110 1000...000
- Double Precision = 1 01111111110 1000...000
📝single-precision float인 1 10000001 01000...000가 십진수로는 ?
- 주어진 부동소수점 표현
- 부호(S) = 1
- 지수 = 10000001 (129)
- 가수 = 01000...000
- 정규화
- 부호(S) = 1 → -1
- 지수 = 129 - 127 = 2 → 2² = 4
- 가수 = 1.01 → 1+2⁻² = 1 + 0.25 = 1.25
- 결론
- x = (-1)¹ * 1.25 * 2² = -1 * 1.25 * 4 = -5.0
📋Quiz!
5.625(10진수)의 부동소수점 저장모습을 적어보시오 (단일 정밀도 형식)
- 5 → 101(2)
- 0.625 → 0.625 * 2 = 1.25 → 1
- 0.25 → 0.25 * 2 = 0.5 → 0
- 0.5 → 0.5 * 2 = 1.0 → 1
- 5.625 = 101.101
- 정규화 → 1.01101 * 2²
- 지수 = 2 + 127 = 129 → 1000 0001
📋Quiz!
다음과 같이 저장된 부동소수점 수가 있다. 십진수로 어떻게 되는지 적어보시오(단일정밀도)
- 1 10000011 00100000..
- 10000011 → 131
- (-1)¹ x (1+0.001) x 2¹³¹⁻¹²⁷ = (-1) x (1 + 0.125)x2⁴ = -18.0
📋Quiz!
다음 수의 저장모습을 적어보시오(단일 정밀도) 23.875(10)
- 23 → 10111(2)
- 0.875 → 0.875 * 2 = 1.75 → 1
- 0.75 → 0.75 * 2 = 1.5 → 1
- 0.5 → 0.5 * 2 = 1.0 → 1
- 23.875 = 10111.111
- 정규화 → 1.0111111 * 2⁴
- 지수 = 4 + 127 = 131
결과 : 0 10000011 0111111000...
📋Quiz!
다음 부동소수점 수 저장모습을 보고 십진수로 변환해보시오(단일 정밀도)
0 10000100 01011000....
10000100 → 132
0.01011 = 0.25 + 0.0625 + 0.03125 = 0.34375
→ (-1) * (1.34375)* 2¹³²⁻¹²⁷ = 43.0 (.0무조건 써야함 43이라고 쓰면 감점)
📌 Denormal Numbers
비정규 숫자
- exponent(지수)가 000...000이라면
- 숨겨진 비트 1.이 사라지고 대신 0. + Fraction 형태로 계산
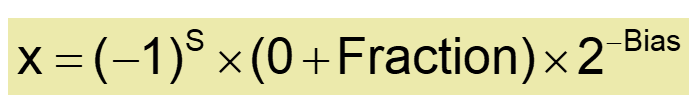
- 사용목적
- 정규 숫자보다 작은 값을 표현하기 위해 사용됨
- 정밀도를 줄여서 작은값을 근사적으로 표현함 ( 예 : 2⁻¹²⁶ 보다 작은값을 표현할때 사용)
만약 Fraction이 모두 0인 경우
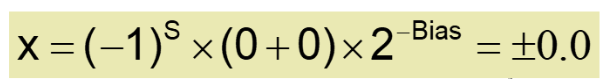
📌 Infinities and NaNs
무한대와 숫자가 아님(Not a Number)
- 무한대
- Exponent = 111.....11
- Fraction = 000..0
- 계산 중 오버플로우가 발생하면 결과로 무한대가 저장됨
- 무한대는 부동소수점 연산에서 일종의 값으로 취급되어 계산을 중지하지 않고 계속 사용가능하다
- (무한대에 어떤 값을 더하거나 빼도 무한대)
- NaN
- Exponent = 111...11
- Fraction = 000...00
- NaN = 숫자가 아님
- 계산이 정의되지 않은 상황에서 발생한다 (0/0, ∞ - ∞같은 상황)
- 무한대 처럼 에러를 처리하거나 계산을 중단하지 않고 연산을 계속 수행할 수 있게 하지만 결과는 항상 NaN
📌 Floating-Point Addition
부동소수점 덧셈
- 10진수 소숫점 4자리의 예시(9.999 * 10¹ + 1.610 * 10⁻¹)
- 소숫점 정렬(작은 수를 큰 수에 맞춤)
- 9.999 * 10¹그대로 둠
- 1.610 * 10⁻¹을 0.0161 * 10¹
- 가수끼리 더함
- 9.999 + 0.0161 = 10.0151
- 결과 = 10.0151 * 10¹
- 결과를 정규화
- 가수가 1이상 10미만이 되도록 조정하는 과정
- 10.0151 * 10¹ → 1.00151 * 10²
- 결과 검증
- 오버플로우 또는 언더플로우가 발생했는지 확인
- 필요하다면 반올림하거나 비정규화 처리 (1.002 * 10²)
- 소숫점 정렬(작은 수를 큰 수에 맞춤)
💡이 순서도 알아두기
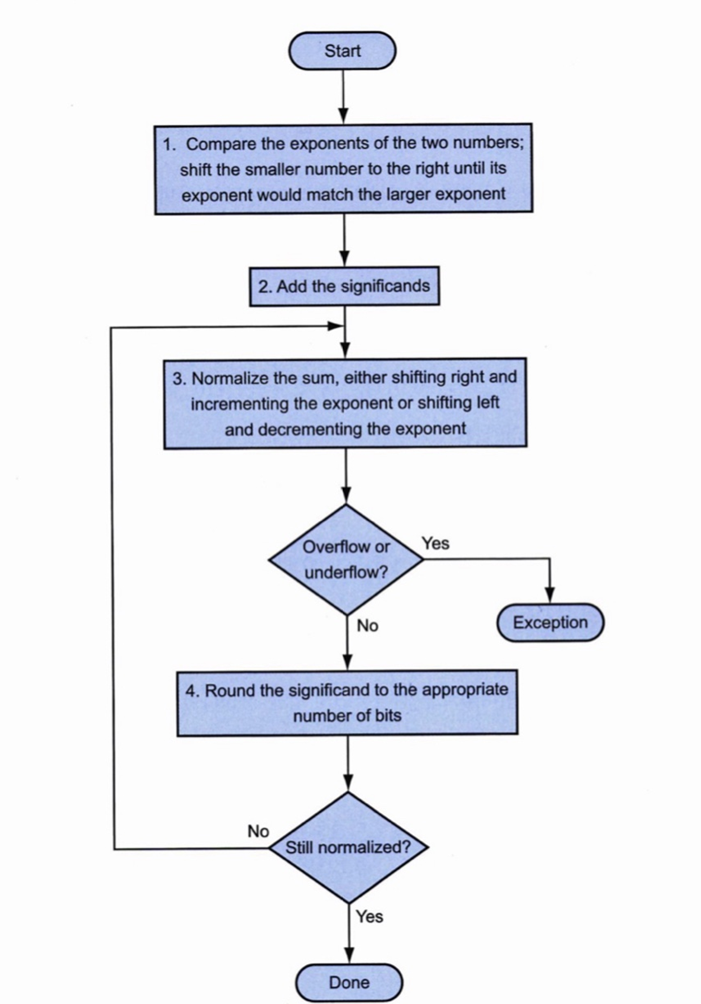
- 두 지수를 비교
- 유효숫자 더하기
- 합을 정규화 & 오버 언더 확인
- 유효 숫자 자리수(비트)에 맞춰 반올림
- 정규화 되었는지 확인(안됐으면 3번으로)
- 종료
binary 소숫점 4자리의 예시(1.000 * 2⁻¹ + -1.110 * 2⁻² = 0.5 + -0.4375)
- 소숫점 정렬(작은 수를 큰 수에 맞춤)
- 1.000 * 2⁻¹ 그대로 둠
- -1.110 * 2⁻² 을 -0.1110 * 2⁻¹
- 가수끼리 더함
- 1.000 + -0.1110 = 0.001
- 결과 = 0.001 * 2⁻¹
- 결과를 정규화
- 가수가 1이상 2미만이 되도록 조정하는 과정
- 0.001 * 2⁻¹ → 1.000 * 2⁻⁴
- 결과 검증
- 오버플로우 또는 언더플로우가 발생했는지 확인
- 필요하다면 반올림하거나 비정규화 처리 (1.002 * 10²)
- 따라서, 2⁻⁴ = 0.0625가 된다
📋Quiz!
다음 부동소수점 수의 덧셈 과정을 이진수를 이용해 보이시오 (4자리 사용한다고 가정)
0.8125 + (-0.1875)
- 소수점 정렬 ( 지수 일치시키기)
- 1.101 * 2⁻¹ + (-.0.011) * 2⁻¹
- 유효숫자 덧셈
- 덧셈결과 : 1.010 * 2⁻¹
- 정규화(이미 정규화된 모습) 및 오버언더 체크
- 1.010 * 2⁻¹
- 자릿수에 맞춰 반올림, 재정규화(는 필요없음)
- 1.010 * 2⁻¹ = 0.625
📌FP Adder Hardware
부동소수점 가산기
- integer adder(정수 가산기)보다 훨씬 더 복잡함
- 한번의 clock cycle 안에 작업하기엔, cycle이 아주 오래 걸리게(느리게) 될 수 있음
- integer operation보다 훨씬 느림
- 느린 clock은 전체 instruction들을 전체적으로 느리게 만듦
- 따라서, FP adder은 일반적으로 여러번의 cycle로 동작한다
- pipeline화(병렬적으로) 될 수 있다
- 하나의 명령에는 여러 cycle이 걸리지만 throughput을 높여 여러개의 명령어를 동시에 실행해 단위 시간당 FP adder의 가능한 작업수가 늘어난다
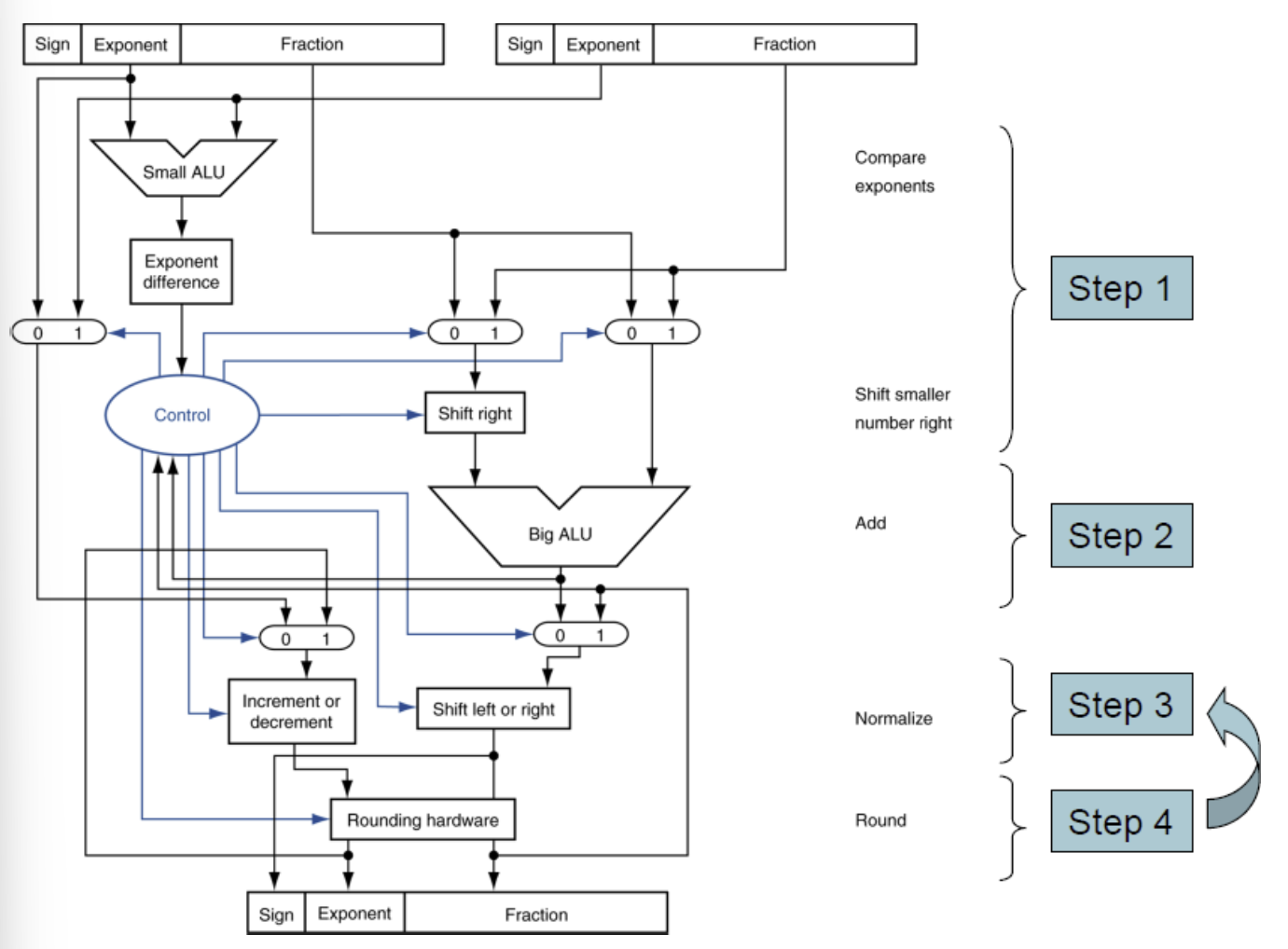
💡순서 봐두기
- 지수비교
- 더 작은 수를 이동
- 유효숫자 더하기
- 정규화
- 반올림
📌Floating-Point Multiplication
부동소수점 곱셈
10진수 소숫점 4자리의 예시(1.110 * 10¹⁰ + 9.200 * 10⁻⁵)
- 두 수의 지수 더하기
- 새로운 지수 = 10 + -5 = 5
- 유효숫자 곱하기
- 1.110 * 9.200 = 10.212 → 10.212 * 10⁵
- 결과를 정규화 오버언더 확인
- 1.0212 * 10⁶
- 반올림 , 필요시 재정규화
- 1.021 * 10⁶
- 부호 결정
- +1.021 * 10⁶
binary 소숫점 4자리의 예시(1.000 * 2⁻¹ + -1.110 * 2⁻² = 0.5 + -0.4375)
- 두 수의 지수 더하기
- unbiased : -1 + -2 = -3
- Biased : (-1 + 127) + (-2 + 127) = -3 + 254 -127 = -3 + 127
- 유효숫자 곱하기
- 1.000 * 1.110 = 1.110 → 1.110 * 2⁻³
- 결과를 정규화하고 , 오버플로우/언더플로우 하지 않았는지 검사
- 1.110 * 2⁻³
- 필요하다면 반올림하거나 비정규화한다
- 1.110 * 2⁻³ → 0.21875
- 피 연산자들의 부호로부터 결과부호를 결정 (+ve * -ve = -ve)
- 1.110 * 2⁻³ = -0.21875
📋Quiz!
다음 부동소수점 수들의 곱을 구하시오(이진수를 이용하고 4자리를 이용)
0.375 * -0.75
- 2진수 변환) 0.011 * 0.110
- 정규화) 1.100 * 2⁻² * 1.100 * 2⁻¹
- 지수더하기 -2 + -1 =-3
- 유효숫자 곱하기 1.100(2) * 1.100(2) → 1.5*1.5=2.25(10) → 10.01(2) 결론→ 10.01 * 2⁻³
- 정규화 1.001 * 2⁻²
- 반올림(변화없음) 1.001 * 2⁻²
- 부호결정 -1.001 * 2⁻² → -0.28125
0.875 * -0.75
- 2진수 변환) 0.111 * 0.11
- 정규화) 1.11 * 2⁻¹ * 1.1 * 2⁻¹
- 지수더하기 -1 + -1 =-2
- 유효숫자 곱하기 1.11(2) * 1.1(2) → 1.75*1.5=2.625(10) → 10.101(2) 결론→ 10.101 * 2⁻²
- 정규화 1.0101 * 2⁻³
- 반올림(변화없음) 1.0101 * 2⁻³
- 부호결정 -1.0101 * 2⁻³ → -0.65625
📌 FP Arithmetic Hardware
부동소수점 산술 하드웨어
- FP multiplier(곱셈기)의 복잡도는 FP adder(가산기)와 비슷하다
- 하지만, adder에서는 유효숫자끼리 더했지만, multiplier은 곱한다
- FP 산술 하드웨어는 보통 다음 기능들을 지원한다
- 덧셈,뺄셈, 곱셈, 나눗셈, 역수, 분모, 제곱...
- FP operation은 일반적으로 여러번의 cycle로 동작한다(병렬적으로 될수있음)
📌 FP Instructions in MIPS
MIPS의 부동소수점 명령어
- FP 하드웨어는 보조 프로세서1
- adjunct Processor : 명령어 집합을 확장하는 보조프로세서
- Coprocessors : CPU와는 별도로 독립된 레지스터 파일을 가진 실행 유닛
- MIPS 구조 : 최대 4개의 보조 프로세서 유닛(0~3번)을 정의
- 독립적인 FP 레지스터 파일
- 32개의 단정밀도 레지스터 : $f0, $f1, .. $f31
- 배정밀도로 사용할 경우 쌍으로 사용 : $f0/ $f1, $f2/$f3 ...
- MIPS ISA Release 2는 32개의 64비트 FP 레지스터를 지원
- FP 명령어는 FP레지스터에서만 작동
- 일반적으로 프로그램은 정수 데이터에 대해 FP 연산을 수행하지 않으며 FP데이터에 대해 정수연산도 수행안함
- FP레지스터는 코드 크기에 최소한의 영향을 주며 더 많은 레지스터를 제공
📌 FP Instructions in MIPS
- FP 로드 및 저장 명령어
- 명령어 : lwc1, swc1, ldc1, sdc1
- 예시 :
ldc1 $f8, 32($sp)
// $f8 : 부동소수점 레지스터- 단정밀도 산술연산
- 명령어: add.s, sub.s , mul.s, div.s
- 예시:
add.s $f0, $f1, $f6
- 배정밀도 산술 연산
- add.d, sub.d, mul.d, div.d
- 예시 :
mul.d $f4, $f4, $f6- 단정밀도 및 배정밀도 비교연산
- 명령어 : c.xx.s, c.xx.d (xx는 비교조건(eq:같음, lt:작음, le : 작거나 같음)
- FP 조건 코드 비트 설정 또는 해제
- 예시 :
c.lt.s $f3, $f4
//$f3 < $f4- FP 조건 코드에 따른 분기
- bclt, bclf (조건이 bclt(참) , bclf(거짓)일때 분기
- 예시 :
bc1t TargetLabel
//참이면 TargetLable로 이동
📌FP Example : ºF to ºC
- c코드
float f2c(float fahr) {
return ((5.0 / 9.0) * (fahr - 32.0));
}
//fahr, result -> $f12, $f0
//literals -> global memory space
- compiled MIPS code:
f2c:
lwc1 $f16, const5($gp) # $f16에 상수 5.0 로드
lwc2 $f18, const9($gp) # $f18에 상수 9.0 로드
div.s $f16, $f16, $f18 # $f16 = 5.0 / 9.0
lwc1 $f18, const32($gp) # $f18에 상수 32.0 로드
sub.s $f18, $f12, $f18 # $f18 = fahr - 32.0
mul.s $f0, $f16, $f18 # $f0 = (5.0 / 9.0) * (fahr - 32.0)
jr $ra # 호출된 함수로 복귀
📌FP Example : array Multiplication
- X = X + Y *Z (모두 32*32, 64bit double-precision elements)
- c 코드
void mm (double x[][], double y[][], double z[][]) {
int i, j, k;
for (i = 0; i != 32; i = i + 1)
for (j = 0; j != 32; j = j + 1)
for (k = 0; k != 32; k = k + 1)
x[i][j] = x[i][j] + y[i][k] * z[k][j];
}
//x,y,z -> $a0, $a1, $a2
//i,j,k -> $s0, $s1, $s2
- MIPS 행렬 곱셈을 수행하는 구체적인 코드 예제를 보여줍니다
li $t1, 32 # 행렬 크기 = 32
li $s0, 0 # i = 0
L1: li $s1, 0 # j = 0
L2: li $s2, 0 # k = 0
//주소 계산(행렬 x의 요소 주소 계산)
sll $t2, $s0, 5 # $t2 = i * 32
addu $t2, $t2, $s1 # $t2 = i * 32 + j
sll $t2, $t2, 3 # $t2 = byte offset of x[i][j]
addu $t2, $a0, $t2 # $t2 = base address + offset
l.d $f4, 0($t2) # $f4 = x[i][j]
//행렬 y와 z의 요소 주소 계산
sll $t0, $s0, 5 # $t0 = i * 32
addu $t0, $t0, $s2 # $t0 = i * 32 + k
sll $t0, $t0, 3 # $t0 = byte offset of y[i][k]
addu $t0, $a1, $t0 # $t0 = base address + offset
l.d $f18, 0($t0) # $f18 = y[i][k]
sll $t0, $s2, 5 # $t0 = k * 32
addu $t0, $t0, $s1 # $t0 = k * 32 + j
sll $t0, $t0, 3 # $t0 = byte offset of z[k][j]
addu $t0, $a2, $t0 # $t0 = base address + offset
l.d $f16, 0($t0) # $f16 = z[k][j]
//연산 수행
mul.d $f16, $f18, $f16 # $f16 = y[i][k] * z[k][j]
add.d $f4, $f4, $f16 # $f4 = x[i][j] + y[i][k] * z[k][j]
//루프 반복
addiu $s2, $s2, 1 # k = k + 1
bne $s2, $t1, L3 # k != 32 -> L3
s.d $f4, 0($t2) # x[i][j] = $f4
addiu $s1, $s1, 1 # j = j + 1
bne $s1, $t1, L2 # j != 32 -> L2
addiu $s0, $s0, 1 # i = i + 1
bne $s0, $t1, L1 # i != 32 -> L1
📌 Accurate Arithmetic (정확한 산술)
- IEEE Std. 754와 추가적인 정밀도
- 보호비트(Guard bit), 자리 맞춤비트(Round bit), Sticky bit
- 연산중 발생하는 추가적인 비트를 통해 정밀도를 높이고 반올림의 정확성을 확보
- 반올림 모드
- 프로그래머스 제어 허용
- 보호비트(Guard bit), 자리 맞춤비트(Round bit), Sticky bit
- 모든 FP유닛이 옵션을 구현하지는 않음 -> 대부분의 프로그래밍 언어는 FP라이브러리는 기본값을 사용함
- 트레이드 오프
- 하드웨어 복잡성, 성능, 시장요구 사이에서 균형을 맞춰야함
- FMA (Fused Multiply Add)
- 곱셈과 덧셈을 하나의 부동소수점 명령으로 수행하는 기능
- 단 한번의 반올림 : 곱셈과 덧셈이 끝난 후 한번만 반올림을 수행해 정확도를 향상
- 고정밀도 제공 : 별도의 곱셈과 덧셈을 수행하는 것보다 정밀도가 높음
- 2 FLOPs(부동소수점 연산) per instruction : 곱셈과 덧셈을 한번에 처리
- 예시: madd.d fd, fr, fs, ft
📍?<궁금한점>📍
🔎 초과 표현
지수에 Bias(편향값)을 더해 음수지수도 표현할 수 있게 하는 방식
🔎부동소수점 표현에서 가수 계산예제에서 1.5가 아니라 왜 1.625로 계산해야할까?
- 부동소수점에서 정규화된 형태는 항상 1.xxx의 형태로 나타낸다
- 즉, 정규화된 형식에서는 항상 가수부분이 1로 시작해야한다
🔎 소수부분 2진수 구하는 법
0.75
- 0.75 * 2 = 1.5 → 1
- 0.5 * 2 = 1.0 → 1
즉, 0.11
🔎 무한대가 중요한 이유
무한대는 에러를 방지하는 메커니즘으로 사용된다
- 일반적으로 연산에서 오버플로우가 발생하면 프로그램이 중단 될 수 있다
- 그러나 부동소수점 표준(IEEE 754)에서는 무한대를 값으로 정의해 계산을 계속 진행할 수 있게한다
- 다만, ∞ - ∞은 NaN이 된
'컴퓨터구조 및 설계 > 3장. Arithmetic for Computers' 카테고리의 다른 글
| 3.7 실례: x86의 SSE와 AVK (1) | 2024.11.20 |
|---|---|
| 3.4 Division (0) | 2024.11.18 |
| 3.3 Multiplication (1) | 2024.11.18 |
| 3.2 Addition and Subtraction (0) | 2024.11.17 |
| 3.1 Introduction (0) | 2024.11.17 |




