leehyeon-dv 님의 블로그
3.2 Addition and Subtraction 본문
cs/컴퓨터구조 및 설계-3장. Arithmetic for Computers
3.2 Addition and Subtraction
leehyeon-dv 2024. 11. 17. 17:47🔑Table of Contents
- Integer Addition - 정수형덧셈
- Integer Subtraction - 정수형 뺄셈
- Dealing with Overflow - 오버플로우 처리
- Arithmetic for Multimedia
- 궁금한점
📌Integer Addition
정수형 덧셈
- 예시)
7(0b111) + 6(0b110) = 13(0b1101)
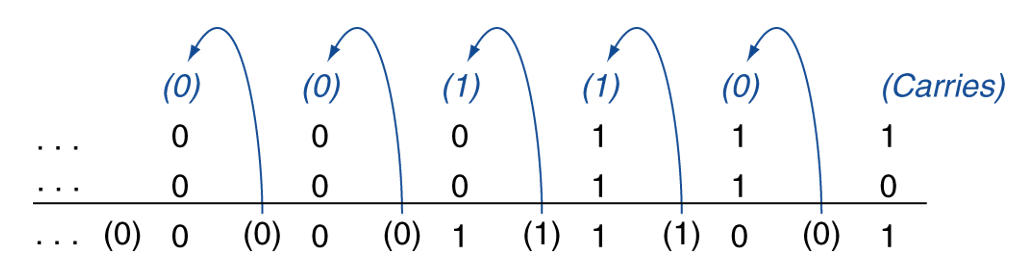
- 만약 결과가 정수형 표현 가능한 범위를 벗어나면 오버 플로우가 일어난다
- 피연산자가 양의값(+ve)과 음의 값(-ve)인 덧셈에서는 오버플로우가 발생하지 않는다
- 피연산자 2개 모두 양의 값(+ve)라면, 발생 할 수 있다
- 부호비트(MSB)로 1이 넘어가면서 음수화
- 피연산자 2개 모두 음의 값(-ve)이라면, 발생할 수도 있다 (underflow)
- 부호비트(MSB)가 1에서, 1이 넘어오면서 0이되어 양수화
📌 Integer Subtraction
정수형 뺄셈
- 2번째 피연산자(operand)를 음수로 만들고 비트덧셈
- 예 ( 7 - 6 = 7 + (-6) = 1)
- +7: 0000 0000 .... 0000 0111
- -6: 1111 1111 .... 1111 1010
- --------------------------------------------
- -1: 0000 0000 .... 0000 0001
📌 Dealing with Overflow
- 몇몇 언어에서는 오버플로우를 무시한다(일어나도 그 값으로 둔다)
- MIPS instruction에서는 addu, addui, subu가 무시
- 다른 언어는 예외를 발생시킨다
- MIPS instruction에서는 add, addi, sub가 예외 발생시킴
- 오버플로우가 발생하면, 예외처리기(Handler) 호출
- 현재 PC를 EPC에 저장
- 예외가 발생할때, 현재 명령어의 주소를 EPC 레지스터에 저장(exception program counter)
- 예외 처리기(Handler)로 점프
- mfc0 명령어로 EPC 값 읽기 (EPC값을 레지스터로 가져옴)
- 예외 처리가 끝난후 EPC 값으로 복귀
📌 Arithmetic for Multimedia
멀티 미디어를 위한 산술
- 그래픽과 미디어 데이터는 8 bit, 16 bit 데이터의 벡터기반 작업을 수행한다
- (64 비트 Adder을 사용한, 분할된 캐리체인)
- 8개의 8bit 데이터 연산
- 4개의 16bit 데이터 연산
- 2개의 32bit 데이터 연산
- SIMD(single Instruction Multiple Data)
- 단일 명령어로 여러개의 데이터를 동시에 계산가능해, 멀티미디어 데이터 처리에 효율적이다
- (64 비트 Adder을 사용한, 분할된 캐리체인)
- Saturating Arithmetic (포화산술연산)
- 오버플로우가 발생시, 값이 최대치에서 멈추도록한다 (2의 보수 산술연산은 오버플로우 발생시 값이 반대로 돌아간다, 하지만 saturating Arithmetic에서는 최대값에서 멈춰 넘치지 않도록한다)
- 예 ) 오디오 클리핑, 비디오의 채도
📍?<궁금한점>📍
🔎그래픽과 미디어 데이터
- 그래픽과 미디어 데이터는 주로 8비트, 16비트 등의 작은 데이터 크기로 이루어져있다
- 이런 데이터는 벡터 기반 연산으로 한꺼번에 여러값을 처리하는 것이 효율적이다
728x90
'cs > 컴퓨터구조 및 설계-3장. Arithmetic for Computers' 카테고리의 다른 글
| 3.7 실례: x86의 SSE와 AVK (1) | 2024.11.20 |
|---|---|
| 3.5 Floating Point (0) | 2024.11.20 |
| 3.4 Division (0) | 2024.11.18 |
| 3.3 Multiplication (1) | 2024.11.18 |
| 3.1 Introduction (0) | 2024.11.17 |



